Maximizing Returns: A Smart Withdrawal Strategy for Lump Sum Investments

Investing a lump sum of money can be a great way to grow wealth, especially when leveraging interest rates effectively. However, many investors struggle to determine the best withdrawal strategy to maximize returns while ensuring a steady cash flow. This article explores a mathematical approach to withdrawing funds in a structured manner while still benefiting from compounding interest.

Understanding the Strategy

The core idea of this strategy is to distribute withdrawals over a fixed period while ensuring the remaining balance continues to earn interest. The process involves:

Applying Interest: The initial lump sum is increased by a fixed annual interest rate.
Withdrawals Based on Remaining Months: Each month, a withdrawal is made based on the remaining months, ensuring a balanced cash flow.
Adjusting for Interest Growth: After each withdrawal, the remaining amount continues to earn interest.

Mathematical Breakdown

Let’s consider an example where:

You invest $50,000 with an annual interest rate of 10%.
The investment period is 12 months.
At the start, the total balance increases to $50,416.67 due to interest.
The first month’s withdrawal is $50,416.67 / 12.
After withdrawal, the remaining balance earns monthly interest, and the next withdrawal is calculated based on the new balance divided by the remaining months.

Using this structured withdrawal method, the total profit from interest accrual over 12 months is approximately $2,792.84.

Advantages of This Approach

Optimized Interest Gains: Unlike fixed withdrawals, this method maximizes the interest earned over time.
Consistent Payouts: Ensures a steady flow of cash while maintaining the value of the investment.
Ideal for Retirement or Passive Income: This can be applied in scenarios where controlled withdrawals are needed while maintaining investment growth.

Mathematical Approach

P = 50,000 (Initial Lump Sum)
r = 10% annual interest rate (r=0.1)
n = 12 months

Step-by-Step Breakdown:

Interest Application

Since the interest is annual, the monthly interest rate is:

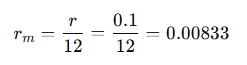
Applying Interest Before First Withdrawal

Since interest compounds monthly, the initial amount grows before the first withdrawal:

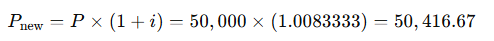
Thus, the total balance at the start of the withdrawal period is $50,416.67.

First Withdrawal

Each month, we withdraw an equal fraction of the remaining balance divided by the months left:

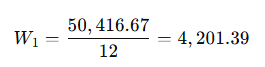
After withdrawing $4,201.39$, the new balance becomes:

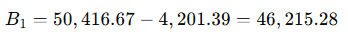
Applying Interest After First Withdrawal

The remaining balance earns interest:

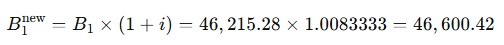
The next withdrawal is based on this new balance, divided by the remaining months (11):

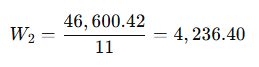
Repeat for Each Month

This process continues, where each month:

Interest is applied to the remaining balance.
A withdrawal is made based on the new balance divided by the remaining months.

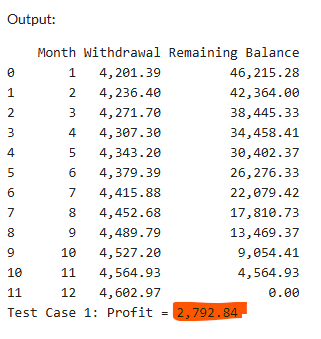
At the end of 12 months, the accumulated withdrawals plus interest earnings lead to a total profit of $2,792.84 over the year.

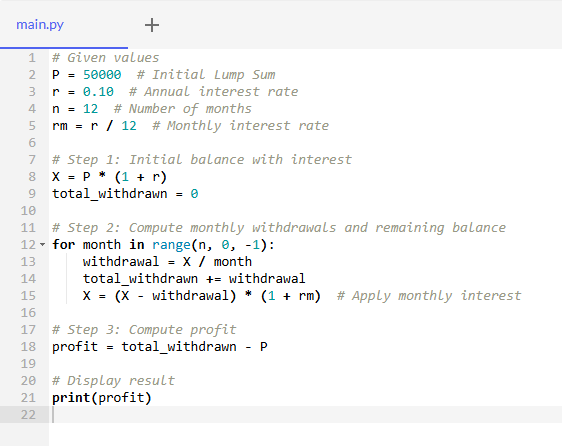
Python script

Let’s calculate the exact value using Python. To modify and run the code use https://onecompiler.com/python/

from decimal import Decimal, ROUND_HALF_UP
import pandas as pd

def calculate_profit_with_breakdown(P, r):
    P = Decimal(P)  # Convert to Decimal for accuracy
    r = Decimal(r)
    n = 12
    rm = r / Decimal(n)  # Monthly interest rate

    # Step 1: Initial balance
    X = P
    total_withdrawn = Decimal('0')

    # Step 2: Compute monthly withdrawals and remaining balance
    breakdown = []
    for month in range(int(n), 0, -1):
        withdrawal = (X * (1 + rm)) / Decimal(month)
        total_withdrawn += withdrawal
        X = (X* (1 + rm)) - withdrawal
        breakdown.append(
          {
            "Month": int(n) - month + 1, 
            "Withdrawal": "{:,}".format(withdrawal.quantize(Decimal('0.01'), rounding=ROUND_HALF_UP)), 
            "Remaining Balance": "{:,}".format(X.quantize(Decimal('0.01'), rounding=ROUND_HALF_UP))
          }
        )
        
    # Step 3: Compute profit
    profit = total_withdrawn - P

    # Convert breakdown to DataFrame and print
    df = pd.DataFrame(breakdown)
    print(df)

    return "{:,}".format(profit.quantize(Decimal('0.01'), rounding=ROUND_HALF_UP))

# Test cases
test_cases = [
    {"P": 50000, "r": 0.10} #50k, annual interest 10%, withdraw every month
]

# Running tests
for i, test in enumerate(test_cases, 1):
    result = calculate_profit_with_breakdown(test["P"], test["r"])
    print(f"Test Case {i}: Profit = {result}")

The result after compiling the Python code:

Conclusion

Withdrawing from a lump sum investment using this structured approach allows you to make the most of compounding interest while securing a steady cash flow. Whether planning for retirement or supplementing income, this method provides a mathematically sound strategy to optimize financial outcomes.

Money Pulse